Dans cet article, nous examinerons une stratégie intéressante connue sous le nom de pari avec supériorité. C'est plus compliqué que surebet et comporte plus de risques, mais cela offre également certains avantages.
Jetons un coup d'œil à la « cuisine » des bookmakers.
Imaginez une pièce, une pièce ordinaire avec deux faces : face et pile. Supposons que quelqu'un parie qu'il peut deviner quelle face de la pièce sera visible après l'avoir lancée. Il est évident que la probabilité que la pièce tombe d'un côté ou de l'autre est de 50/50. Il sera donc juste de définir des cotes à 2 pour la face et 2 pour la pile. Cela signifie que si deux joueurs parient et mettent un dollar sur des résultats différents, le gagnant recevra 2 dollars et le perdant ne recevra rien.
Cependant, les bookmakers ne font jamais cela. Dans le meilleur des cas, un bookmaker fixera une cote de 1,9 pour la face et 1,9 pour la pile. Si nos joueurs placent leurs paris via un bookmaker et parient également 1 dollar chacun, le gagnant ne recevra que 1,90 $, car 0,10 $ seront versés au titre de la commission du bookmaker. C'est ce qu'on appelle une marge. Et c'est ainsi que les bookmakers vivent.
Dans un monde idéal et dans une situation où un bookmaker paiera tout l'argent des paris comme prix, les cotes des événements devraient se corréler d'une certaine manière :
1/K1 + 1/K2 + … + 1/Kn = 1
Ici K1, K2, … Kn sont les cotes pour chacun des n résultats opposés de l'événement - par exemple, paris 1, X, 2. Chacune des cotes doit être égale à 1 divisé par la probabilité d'un résultat correspondant.
Cependant, si nous prenons une ligne réelle de n'importe quel bookmaker et calculons la somme des probabilités, elle ne sera pas égale à 1. Prenons comme exemple les cotes de Bwin pour un match de l'Inter Milan – Porto.
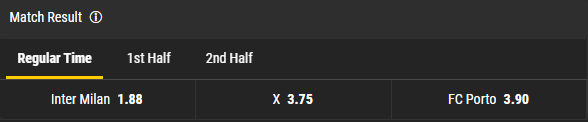
1/1.88 + 1/3.75 + 1/3.90 = 1.054 ( > 1 !!! )
(1.054 - 1) * 100% = 5.4% marge
Par conséquent, les bookmakers fixent toujours leurs cotes de manière à leur donner un avantage sur les joueurs. Ils baissent les cotes en tenant compte de leurs revenus. La probabilité est du côté du bookmaker. C'est pourquoi la majorité (environ 98 %) des joueurs ordinaires, pariant « pour la chance », perdent leur banque dans le long terme.
Comme vous pouvez le voir dans la description de la marge, chaque bookmaker essaie de deviner la probabilité de tel ou tel résultat et fixe donc de faibles cotes. Cependant, il arrive parfois que les bookmakers commettent des erreurs et fixent au contraire des cotes élevées.
Revenons à notre exemple de lancer de pièce, supposons que le bookmaker a décidé que la face serait plus susceptible de sortir et a fixé des cotes de 2,1 sur la face et 1,75 sur la pile. Il est clair que le bookmaker a tort. Si un joueur sait que la probabilité des deux résultats est exactement de 50 %, il sera beaucoup mieux de parier sur la face.
Si le joueur place 100 paris comme celui-ci, pariant un dollar chaque fois, il gagnera avec une probabilité de 50 %. Par conséquent, le joueur gagnera 100 х 50% х 2,1 = 105 dollars. Avec un nombre suffisamment important de paris avec supériorité, le joueur aura un profit de 5%. Comme la loi de la probabilité est du côté du joueur dans ce cas, sa banque augmentera à long terme.
Pour illustrer cette idée, utilisons un autre exemple, cette fois avec un dé. Il est évident que la probabilité de lancer n'importe quel nombre est de 1 sur 6. Faisons jouer deux joueurs en suivant les règles suivantes : le premier pense à un nombre et lance le dé. S'il gagne, il reçoit 5 dollars de l'autre. S'il perd, il donne à l'autre un dollar. Il est clair que le premier joueur n'aura bientôt rien (à part un trou dans la poche). Changeons les règles : si le premier joueur devine le nombre, il gagne 7 dollars. S'il ne le fait pas, il donnera un dollar. Maintenant, le premier joueur va rapidement faire faillite au second.
Un pari avec supériorité est un pari qui rend l'inégalité suivante vraie :
K * Cote > 1
où K est la cote et Cote est la probabilité réelle de ce résultat.
Pour être en mesure de trouver des paris avec supériorité, vous devez d'abord être capable d'évaluer la probabilité réelle des résultats des événements. Après cela, une fois que vous connaissez les vraies probabilités, vous devez trouver les cotes qui rendent l'inégalité K * Cote > 1 vraie.
Il est très difficile de déterminer la probabilité réelle des résultats dans des événements tels qu'un match de football. Les bookmakers embauchent des départements entiers d'analystes professionnels pour prédire les résultats des matchs.
Il existe deux méthodes principales pour prédire les résultats :
La première méthode est largement utilisée par les bookmakers. Ils essaient d'utiliser toutes les données dont ils disposent pour évaluer la chance qu'une certaine équipe gagne. Il y a des parieurs professionnels qui connaissent également très bien les équipes et peuvent prédire les résultats aussi précisément que les bookmakers. La méthode analytique, cependant, nécessite une connaissance approfondie du sujet et est difficilement automatisable.
La deuxième méthode est basée sur les statistiques. Si vous avez les cotes d'un grand nombre de bookmakers, vous pouvez calculer la marge de chaque cote. Vous pouvez ensuite utiliser la marge pour essayer de déterminer comment le bookmaker a évalué la probabilité. Enfin, vous calculez la valeur moyenne - et cela sera la prédiction la plus précise, car elle est basée sur le travail de nombreux analystes. Cette méthode peut sembler moins précise pour certaines personnes, mais elle peut être facilement automatisée.
Notre service utilise l'approche statistique pour trouver des paris avec supériorité.
Une surebet d'un bookmaker possède toujours une propriété intéressante. Si vous supposez que tous les paris d'une certaine surebet appartiennent à un seul bookmaker et que vous calculez la marge, vous obtiendrez un nombre négatif. Vérifions l'une des surebets.
1/2 + 1/3,75 + 1/5 = 0,9667 ( < 1 )
La marge est égale à : (0,9667 - 1) * 100% = -3,33%
Cela signifie qu'au moins l'un des paris de la surebet est surestimé. C'est-à-dire qu'au moins un pari dans n'importe quelle surebet réalisant un profit positif doit être un pari avec supériorité (mais il peut y en avoir davantage). En gros, ce pari surestimé a très probablement donné lieu à la surebet et tous les autres paris sûrs ne sont utilisés que pour soutenir celui-ci.
Ainsi, si vous avez une liste des surebets trouvées pour le même événement, vous pouvez essayer de déterminer quel pari les a causés. Par exemple, si tous les surebets pour le même événement contiennent un pari pour la victoire de la première équipe par le même bookmaker, il est évident que ce pari est surestimé.
Contrairement aux surebets, les paris avec supériorité ont leurs avantages et leurs inconvénients.
Avantages
Moins de paris. Lorsque vous utilisez des surebets, vous devez parier sur tous les résultats de la surebet, et si vous ne pariez pas sur au moins l'un d'eux, vous risquez de perdre tous les autres paris. Lorsque vous jouez avec des paris avec supériorité, vous devez faire un pari par pari avec supériorité, minimisant ainsi le risque de ne pas être en mesure de placer d'autres paris.
Moins de comptes chez les bookmakers. Pour jouer avec des surebets, vous avez besoin d'au moins deux ou trois comptes dans différentes entreprises (mais plus il y en a, mieux c'est). Lorsque vous jouez avec des paris avec supériorité, vous n'avez besoin que d'un seul compte.
Le comportement du joueur est plus naturel. En jouant avec des surebets, le joueur est obligé d'obéir au calculateur et de placer des paris dépendants. Un bookmaker peut trouver étrange qu'un joueur parie toujours quelque chose comme 5,43 $ sur un total de 13,5 dans des matchs comme Honduras – Guadeloupe. Lorsque vous jouez avec des paris avec supériorité, vous pouvez parier n'importe quel montant qui ne contredit pas la stratégie choisie. Cela suscite moins de soupçons.
En théorie, parier avec supériorité est plus rentable que de faire surebet. Étant donné que chaque surebet a également un pari surévalué et des paris de sauvegarde, chaque parieur sur le surebet place des paris sur tous eux, pas seulement sur celui qui peut être rentable. Le joueur achète presque une assurance contre la perte, mais doit la payer à un coût considérable. Si les paris surévalués sont trouvés et utilisés efficacement, le joueur gagnera plus d'argent en moyenne, puisque la marge du bookmaker n'est pas payée.
Inconvénients
